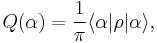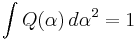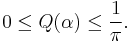Husimi Q representation

The Husimi-Q distribution is a mathematical tool used in physics, and was introduced in 1940.[1] The Q-representation is a quasi-probability distribution commonly used in quantum mechanics[2] and also to represent the quantum state of light. It is used in the field of quantum optics and particularly for tomographic purposes. It is also applied in the study of quantum effects in superconductors.[3]

Definition and properties

The Husimi-Q distribution (called Q-function in the context of quantum optics) is the simplest distribution of quasi-probability in phase space. It is defined as

Q(\alpha)=\frac{1}{\pi}\langle\alpha|\rho|\alpha\rangle,

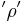which is \pi times the probability distribution for the state '\rho' to be found in the coherent state 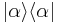|\alpha\rangle \langle \alpha | . It produces a pictorial representation of the state 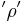'\rho' to illustrate several of its mathematical properties.[4] Essentially, it is a convolution by a phase-space Gaussian distribution of the Wigner quasi-probability distribution.

The Q-distribution is normalized to unity,

\int Q(\alpha)\,d\alpha^2 = 1

and is non-negative definite and bounded:

0 \leq Q(\alpha) \leq \frac{1}{\pi}.

See also

References

  1. ^ Kôdi Husimi (1940). "Some Formal Properties of the Density Matrix", Proc. Phys. Math. Soc. Jpn. 22: 264-314 .
  2. ^ PAM Dirac (1982). The principles of quantum mechanics (Fourth Edition ed.). Oxford UK: Oxford University Press. p. 18 ff. ISBN 0198520115. http://books.google.com/books?id=XehUpGiM6FIC&printsec=frontcover&dq=intitle:quantum+intitle:mechanics+inauthor:dirac&lr=&as_brr=0&sig=mRVsWMu1RsjbysOw2sG2CK_mNpc#PPA20,M1. 
  3. ^ DJE Callaway (1990). "On the remarkable structure of the superconducting intermediate state". Nuclear Physics B 344: 627–645. Bibcode 1990NuPhB.344..627C. doi:10.1016/0550-3213(90)90672-Z. 
  4. ^ Cosmas K. Zachos, David B. Fairlie, and Thomas L. Curtright, Quantum Mechanics in Phase Space, (World Scientific, Singapore, 2005) ISBN 978-981-238-384-6 [1].